For surfaces that have a non-vanishing dipole density quantum-espresso (QE) offers a dipole correction in combination with the sawtooth potential. The relevant variables in the pw.x input are dipfield and tefield, which both have to be set to true. Unfortunately this is not all there is to do – we also have to define where the dipole is located and the location (and size) of the dipole play an important role. Since this confuses me regularly I decided to write it down here in the hope it helps me and others.

Lets assume we have centered the slab in the center of our cell and the cell extends from 0 (the bottom) to 1 (the top). As QE uses periodic boundary conditions everything that exceeds the length of the cell will re-enter the cell at the bottom, i.e. (1+x)=x in relative z-coordinates. As the manual tells us one has to take care of 3 parameters: emaxpos, eopreg and eamp. Since we only want to apply a dipole correction the amplitude eamp=0. The field linearly increases until emaxpos and then decreases to reach 0 at emaxpos+eopreg, as such they represent the positive and negative charges that create the dipole. It is important that the change of slope, that is emaxpos, lies in the vacuum region and so must emaxpos+eopreg (the opposite charge) – otherwise the correction will not work. A very useful setup is to center the slab in the cell (~0.5 in relative z-coordinates) and the dipole around 0 of the slab. One can then slowly increase the length of the dipole and see if the resulting electrostatic potential (plot_num=11 in pp.x) becomes flat in the vacuum region (thanks for Dr. Thomas Brumme for the hint!). As long as the dipole and the charge density of the electrons do not overlap the correction works and the necessary amplitude of the dipole field decreases linearly with the dipole length – as to be expected since p=q*z (see the right side of Figure 1). When the dipole gets too close the correction fails and the potential is no longer flat in the vacuum region. Please note that this does not mean that SCF convergence cannot be reached – in fact, the last case converges faster than all the cases were the results are physically meaningful in this particular case.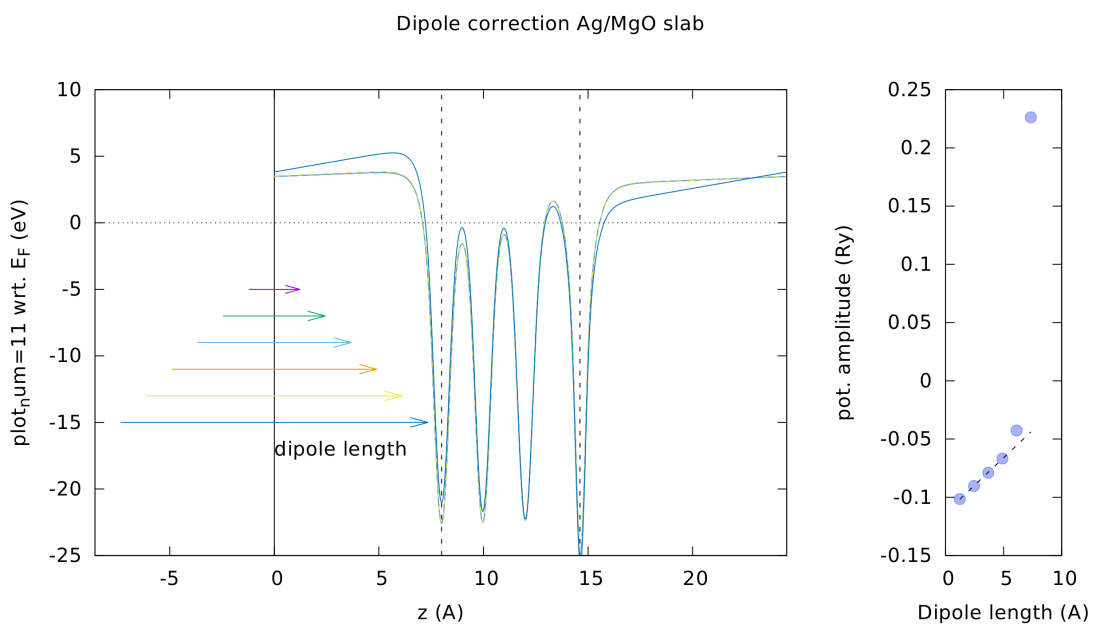

Figure 1. Potential as obtained by pp.x (plot_num=11) and averaged in xy-plane (average.x) as a function of the dipole length with the dipole centered at 0 of the cell. On the right side the amplitude of the dipole field is shown as function of the dipole cell.

In recent versions of QE a different correction has been implemented by Sohier et al. as well. This is activated with the input-flag assume_isolated =’2d’ and gives basically the same result. As an advantage the new correction seems to be working better with phonons of 2-dimensional systems but not all codes that build on QE output are able to read it yet (for example the resulting electron-phonon matrix elements in EPW are too large by a factor of at least 100).

Attached shell script will run a calculation for dipoles of varying length – by collecting the results one can reproduce above figure.

Hope this was helpful – if not, let me know in the comments!

run